Une éolienne est une machine qui, par définition, transforme
l’énergie du vent en énergie mécanique. Pour débuter, il y a lieu de
quantifier la source d’énergie dont on dispose, c’est-à-dire l’énergie
associée au vent. Si le vent présente une certaine vitesse « V » à un
moment donné et traverse une certaine surface « A », la puissance
instantanée du vent est donnée par la relation suivante :
Pvent = 1/2 rho*A*V3,
où « rho » est la masse volumique de l’air, qui vaut approximativement 1.2 kg/m³ à 20°C, au niveau de la mer.
Néanmoins, cette relation met clairement en évidence :- que la puissance disponible du vent à un instant donné dépend du cube de la vitesse du vent. En conclusion, si vous avez un vent 2 x plus rapide, vous avez 8 x plus de puissance. On comprend dès lors tout l’intérêt de placer des éoliennes dans des sites venteux. Ce n’est donc pas un caprice de technicien puriste, on voit que le potentiel d’énergie dépend fortement de la vitesse du vent. C’est une condition nécessaire et non une option.
- que la puissance disponible dépend directement de la surface
traversée par le vent. Si on la considère équivalente à la surface
balayée par le rotor d’une éolienne, la puissance instantanée du vent
(telle qu’évaluée par la relation ci-dessus) représente le maximum de
puissance disponible que l’éolienne peut convertir. On sait que la
surface balayée par une éolienne dépend du rayon de son rotor (π*R²). Du
coup, la puissance disponible dépend du carré du rayon de l’éolienne. En conclusion, si vous avez un rotor 2 x plus long, vous avez 4 x plus de puissance.
[Découvrez ICI >> notre outil de pré dimensionnement éolien]

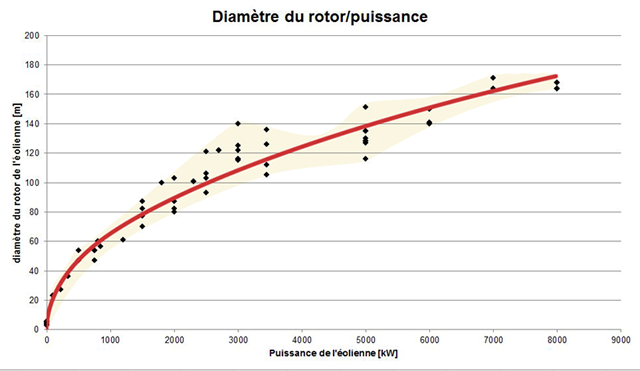
Diagramme illustrant le rapport entre le diamètre du rotor et la puissance maximale de l’éolienne :
Réalisé à partir des fiches techniques de 62 modèles d’éoliennes récentes
Réalisé à partir des fiches techniques de 62 modèles d’éoliennes récentes
- que la masse volumique de l’air a une influence sur la puissance
disponible. On sait que la masse volumique de l’air dépend de la
température, de l’humidité et de la pression atmosphérique. Suivant ces
paramètres, on peut obtenir des variations de 20 % de la masse
volumique et donc de la puissance instantanée du vent.
Ainsi, au niveau de la mer, par – 10 °C un mètre cube d’air pèsera 1,341 kg tandis qu’à 30 °C, il n’en pèsera plus que 1 164 kg.
L’énergie du vent
Connaître la puissance
instantanée du vent est une chose, mais ce qui nous intéresse, c’est son
énergie. Il y a donc une notion de temps qui va devoir intervenir
quelque part. Pour connaître l’énergie du vent sur une période, il faut
intégrer sa puissance sur cette même période. La connaissance de la
vitesse moyenne du vent n’est pas suffisante, il faut disposer de
l’évolution de la vitesse sur la période étudiée et sommer les
contributions.
Prenons une période de 24h et comparons trois journées venteuses avec un vent moyen de 6m/s pour chacune mais un profil de distribution différent :
Prenons une période de 24h et comparons trois journées venteuses avec un vent moyen de 6m/s pour chacune mais un profil de distribution différent :
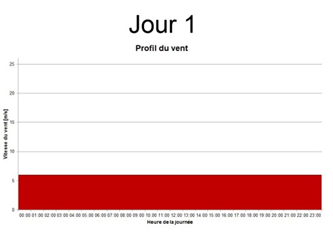
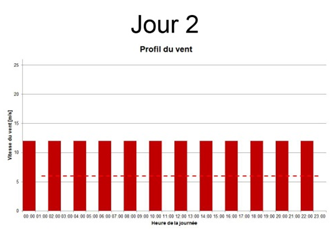
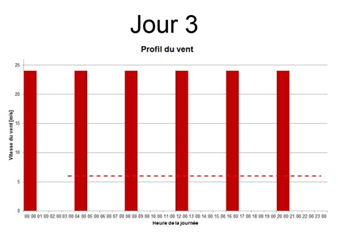
Si les vitesses moyennes sont bien les mêmes, le profil de distribution est lui très différent entre ces trois journées. Un simple calcul nous permet d’observer que la quantité d’énergie que le vent aura fournie sur 24h par m² pour chaque profil est drastiquement différente.
- Jour1 : 24 [h] x 6 [m/s]³ x 1 [m²] x 1,2 [kg/m³] = 6 220 Wh = 6,22 kWh
- Jour2 : 12 [h] x 12 [m/s]³ x 1 [m²] x 1,2 [kg/m³] = 24 880 Wh = 24,88 kWh
- Jour3 : 6 [h] x 24 [m/s]³ x 1 [m²] x 1,2 [kg/m³] = 99 530 Wh = 99.53 kWh !!
Explication avec quelques formules
Supposons que l’on dispose de mesures du vent à intervalles réguliers
pendant une période de plus ou moins une année. L’intervalle entre
chaque mesure est de « dt » secondes et le nombre d’échantillons est de
« N » mesures. La durée de la période d’observation, « T », est donc
N*dt. On obtient un échantillon de différentes vitesses, U1 jusque UN. Il est donc possible d’estimer simplement la vitesse moyenne du vent, Um, pendant cette période de mesure :
Um = (1/N)*(U1+U2+ … + UN-1 + UN)
Pour obtenir l’énergie, il faut sommer les
contributions des différentes mesures. Si la puissance du vent associée à
une mesure de vitesse Ui vaut
Pi = 1/2*rho*A*(Ui)3
L’énergie du vent, Ev, vaut alors : Ev = (P1 + P2 + …. + PN-1 + PN)*dt.
En fait, il faut connaître l’évolution de la vitesse du vent durant
toute la période étudiée. Si on ne connaissait que la vitesse moyenne du
vent, Um, cela ne suffirait pas pour déterminer l’énergie, Ev. En effet, on ne peut pas calculer l’énergie du vent au moyen de la vitesse moyenne (de la manière suivante) :
Ev n’est pas égal à 1/2*rho*A*(Um)3*T
Cette différence sera chiffrée dans la section suivante et elle est loin d’être négligeable.
La distribution du vent : approche statistique
Dans la section précédente,
nous avons intégré les différentes puissances pour obtenir l’énergie du
vent sur la période étudiée. Il existe une autre manière de procéder qui
présente en outre l’avantage de synthétiser les propriétés du vent sur
la période investiguée. Il s’agit de la fonction de distribution du vent, que l’on nommera ici p(V).
Imaginons que l’on s’intéresse aux vitesses prises par le vent. Celles-ci varient entre la valeur zéro et la vitesse maximale rencontrée. On découpe cet intervalle en différentes petites plages de vitesses de largeur dV. Le produit p(V)*dV donne la probabilité que la vitesse du vent aie la valeur V durant la période d’observation (que l’on avait nommée, « T »). Cette valeur oscille entre « 0 » et « 1 ». La valeur est nulle quand le vent n’atteint jamais cette vitesse et la valeur « 1 » quand le vent est toujours à la vitesse V, ce qui, dans la pratique, n’arrive jamais. À titre d’exemple, si la probabilité p(V)*dV que la vitesse soit égale à V est de 0.5, cela veut simplement dire que l’on rencontre la vitesse V la moitié du temps de l’observation. Cela peut paraître assez abstrait, mais il est difficile de passer à côté de ce concept si l’on veut introduire les approches statistiques de l’évaluation de l’énergie du vent.
Une fois cette fonction connue, on peut déterminer la contribution de la vitesse V à l’énergie du vent de la manière suivante :
En conclusion, les fonctions de distribution du vent peuvent avoir deux utilités. D’une part, elles permettent de synthétiser les propriétés d’intérêt du vent en relation avec la production d’énergie et, d’autre part, si on utilise des fonctions prédéfinies comme la fonction de Weibull, elles permettent d’évaluer l’énergie du vent si on ne dispose que de données lacunaires concernant son évolution sur un site donné. Dans ce dernier cas de figure, il faut être conscient que la qualité de cette méthode est moindre qu’une campagne de mesure sur une dizaine d’années. Au mieux, les résultats auront une valeur identique.
Pourquoi ne pas directement évaluer l’énergie au moyen de la vitesse moyenne ? Ce n’est pas la même chose !
La puissance instantanée du vent est obtenue en prenant le cube de la vitesse. On obtient l’énergie sur la période de mesure en intégrant ces puissances. Mathématiquement parlant, c’est différent d’intégrer la vitesse sur la période puis de la mettre au cube. En d’autres termes, l’ordre dans lequel vous réalisez les opérations d’intégration et mise à la puissance 3 a une importante : on met d’abord la vitesse instantanée au cube puis on somme les différentes contributions durant la période analysée.
Fait-on une grosse erreur si on évalue l’énergie du vent au moyen de la vitesse moyenne ? Oui ! Sur base de cas rencontrés, on peut facilement faire une sous-estimation de 100 % voire plus.
On peut essayer de voir ce que cela donne avec la fonction de distribution de Weibull. Avant de rentrer dans le vif du sujet, on peut d’abord se faire une idée de l’évolution de la vitesse moyenne et de la variance en fonction de l’évolution des deux paramètres de la fonction de Weibull, le paramètre de forme, k, et le paramètre d’échelle, c.
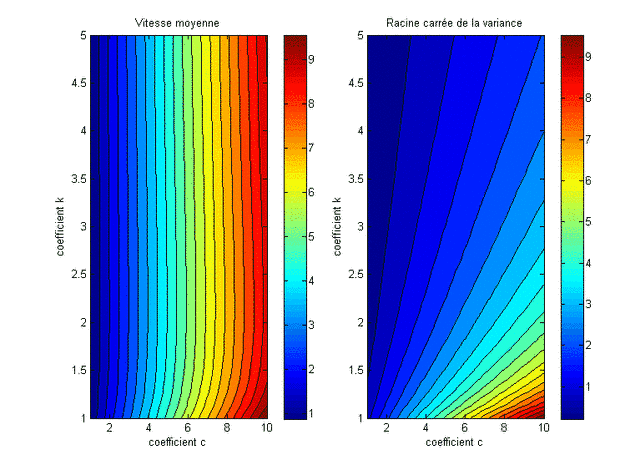
On voit que la vitesse moyenne du vent dépend essentiellement du facteur d’échelle, c. La variance, quant à elle, dépend fortement des deux facteurs. Finalement, on représente maintenant le rapport entre l’énergie du vent calculée avec la fonction de Weibull et l’énergie du vent calculée de façon approximative par la moyenne de la fonction de Weibull. On connaît ce rapport sous le nom de facteur Ke,
Ke = Somme(1/2*rho*A*Ui³/N)/(1/2*rho*A*Um³) = (1/N Somme(Ui³))/(Um³)
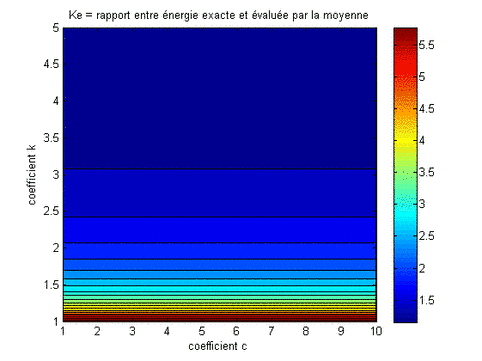
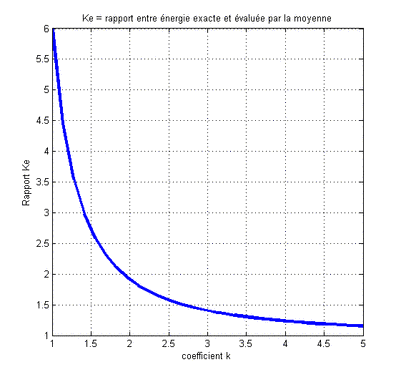
Conclusion, le rapport, Ke, peut être très important, d’autant plus que le facteur de forme k est faible. On aura noté qu’il dépend uniquement de la valeur de ce facteur k. On reprend ci-dessous, un tableau avec des chiffres :
k : 1.2 / 2 / 3 / 5
ke : 3.99 / 1.91 / 1.40 / 1.15.
Courbe caractéristique de puissance et rendement instantané
Le vent présente donc une certaine énergie pendant une période donnée. Cette énergie est convertie par l’éolienne en énergie mécanique et très certainement en énergie électrique. Cette transformation peut être décomposée en plusieurs étapes :
On définit le rendement instantané global d’une éolienne pour une vitesse de vent, V, comme étant le rapport entre la puissance électrique débitée par la génératrice, Pelec, et la puissance instantanée du vent, Pvent :
La puissance nominale d’une éolienne
ne veut rien dire sur son efficacité si le constructeur ne mentionne
pas à quelle vitesse de vent cette puissance électrique est obtenue.
En effet, on n’est pas en mesure de déterminer la puissance instantanée
du vent et donc d’établir son rendement global instantané.
Imaginons que l’on s’intéresse aux vitesses prises par le vent. Celles-ci varient entre la valeur zéro et la vitesse maximale rencontrée. On découpe cet intervalle en différentes petites plages de vitesses de largeur dV. Le produit p(V)*dV donne la probabilité que la vitesse du vent aie la valeur V durant la période d’observation (que l’on avait nommée, « T »). Cette valeur oscille entre « 0 » et « 1 ». La valeur est nulle quand le vent n’atteint jamais cette vitesse et la valeur « 1 » quand le vent est toujours à la vitesse V, ce qui, dans la pratique, n’arrive jamais. À titre d’exemple, si la probabilité p(V)*dV que la vitesse soit égale à V est de 0.5, cela veut simplement dire que l’on rencontre la vitesse V la moitié du temps de l’observation. Cela peut paraître assez abstrait, mais il est difficile de passer à côté de ce concept si l’on veut introduire les approches statistiques de l’évaluation de l’énergie du vent.
Une fois cette fonction connue, on peut déterminer la contribution de la vitesse V à l’énergie du vent de la manière suivante :
Ev(V) = 1/2*rho*A*V3*(p(V)*dV*T)
On obtient alors l’énergie du vent en sommant sur
les différentes gammes de vitesse rencontrées. En d’autres termes,
chaque gamme de vitesses se présente à une certaine fréquence pendant la
période étudiée, « T », et correspond à une certaine contribution à
l’énergie totale. Pour obtenir l’énergie du vent, il faut tenir compte
de toutes les gammes de vitesse rencontrées et de leur contribution.
Comment obtient-on cette fonction de
distribution ? La manière la plus consistante est d’utiliser les valeurs
mesurées de vitesse et de regarder à quelle fréquence les différentes
vitesses sont rencontrées. C’est la situation idéale.
Néanmoins, il arrive que l’on ne dispose pas de
ces mesures ou, du moins, on dispose de mesures lacunaires qui ne
permettent pas d’établir proprement la fonction de distribution. Par
exemple, le potentiel de vent peut varier d’une année à l’autre si bien
qu’il faut plusieurs années de mesure pour établir un comportement
moyen. La littérature reprend souvent le chiffre de 10 années de mesure.
On comprend dès lors qu’une évaluation du potentiel sur une période
aussi longue ne soit pas toujours possible. Dans ce cas de figure, on
peut faire une hypothèse sur la manière dont les vitesses sont
rencontrées dans le temps. Dans le domaine de l’éolien, la fonction la
plus courante est la fonction de distribution de Weibull.

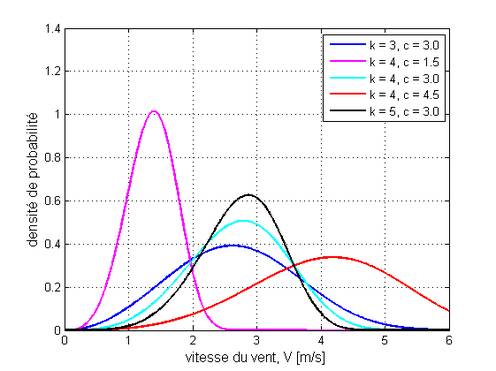
Exemples de distributions de Weibull pour différents jeux de paramètres.
La fonction de Weibull est représentée dans le graphe ci-dessus. Elle ne comporte que deux paramètres : le facteur de forme, k, et le facteur d’échelle,
c. Qu’est-ce que cela veut dire ? Cela veut dire que l’on sait à quelle
fréquence sont rencontrées les différentes vitesses de vent, V, durant
la période d’observation uniquement si l’on est capable de fixer la
valeur de deux coefficients. Le but du jeu est de fixer ces deux
coefficients sur base de données lacunaires dont on dispose. En d’autres
mots, on est capable de reconstruire l’historique d’intérêt du vent sur
la période étudiée uniquement si l’on est capable de fixer les deux
paramètres de la fonction de Weibull : notamment sur base de la vitesse
moyenne du vent et de sa variance. La qualité de cette méthode est
correcte si, effectivement, la distribution du vent a, dans le site
étudié, effectivement tendance à suivre une répartition de Weibull. Cela
devient une question de spécialiste. On invite le lecteur à se référer à
des ouvrages plus approfondis si cette thématique l’intéresse. À noter
que l’on entend aussi parler de la fonction de distribution de Rayleigh
qui est plus simple dans la mesure où elle ne comporte qu’un seul
paramètre (c’est un cas particulier de la fonction de Weibull).
À titre d’exemple, commentons la figure ci-dessus
représentant 5 jeux différents de paramètres pour la fonction de
distribution de Weibull. On voit par exemple la courbe
« rouge » représentant des vents de vitesse moyenne proche de 4.25 et
qui oscille largement autour de cette valeur. La courbe « noire » quant à
elle représente des vents de vitesse moyenne plus faible (proche de
3.5) et qui ont une variation nettement plus faible (proche de 3m/s) et
qui ont une variation nettement plus faible autour de cette moyenne.
En conclusion, les fonctions de distribution du vent peuvent avoir deux utilités. D’une part, elles permettent de synthétiser les propriétés d’intérêt du vent en relation avec la production d’énergie et, d’autre part, si on utilise des fonctions prédéfinies comme la fonction de Weibull, elles permettent d’évaluer l’énergie du vent si on ne dispose que de données lacunaires concernant son évolution sur un site donné. Dans ce dernier cas de figure, il faut être conscient que la qualité de cette méthode est moindre qu’une campagne de mesure sur une dizaine d’années. Au mieux, les résultats auront une valeur identique.
Pourquoi ne pas directement évaluer l’énergie au moyen de la vitesse moyenne ? Ce n’est pas la même chose !
La puissance instantanée du vent est obtenue en prenant le cube de la vitesse. On obtient l’énergie sur la période de mesure en intégrant ces puissances. Mathématiquement parlant, c’est différent d’intégrer la vitesse sur la période puis de la mettre au cube. En d’autres termes, l’ordre dans lequel vous réalisez les opérations d’intégration et mise à la puissance 3 a une importante : on met d’abord la vitesse instantanée au cube puis on somme les différentes contributions durant la période analysée.
Fait-on une grosse erreur si on évalue l’énergie du vent au moyen de la vitesse moyenne ? Oui ! Sur base de cas rencontrés, on peut facilement faire une sous-estimation de 100 % voire plus.
On peut essayer de voir ce que cela donne avec la fonction de distribution de Weibull. Avant de rentrer dans le vif du sujet, on peut d’abord se faire une idée de l’évolution de la vitesse moyenne et de la variance en fonction de l’évolution des deux paramètres de la fonction de Weibull, le paramètre de forme, k, et le paramètre d’échelle, c.

On voit que la vitesse moyenne du vent dépend essentiellement du facteur d’échelle, c. La variance, quant à elle, dépend fortement des deux facteurs. Finalement, on représente maintenant le rapport entre l’énergie du vent calculée avec la fonction de Weibull et l’énergie du vent calculée de façon approximative par la moyenne de la fonction de Weibull. On connaît ce rapport sous le nom de facteur Ke,
Ke = Somme(1/2*rho*A*Ui³/N)/(1/2*rho*A*Um³) = (1/N Somme(Ui³))/(Um³)


Conclusion, le rapport, Ke, peut être très important, d’autant plus que le facteur de forme k est faible. On aura noté qu’il dépend uniquement de la valeur de ce facteur k. On reprend ci-dessous, un tableau avec des chiffres :
k : 1.2 / 2 / 3 / 5
ke : 3.99 / 1.91 / 1.40 / 1.15.
Courbe caractéristique de puissance et rendement instantané
Le vent présente donc une certaine énergie pendant une période donnée. Cette énergie est convertie par l’éolienne en énergie mécanique et très certainement en énergie électrique. Cette transformation peut être décomposée en plusieurs étapes :
- L’énergie cinétique du vent est convertie en travail moteur à l’axe du rotor. Cette conversion est réalisée avec un certain rendement, le rendement aérodynamique.
- Le travail moteur au rotor est transmis vers l’axe de la génératrice avec un certain rendement, le rendement d’accouplement mécanique.
- La génératrice transforme le travail moteur à son axe en énergie électrique avec un certain rendement électrique.
On définit le rendement instantané global d’une éolienne pour une vitesse de vent, V, comme étant le rapport entre la puissance électrique débitée par la génératrice, Pelec, et la puissance instantanée du vent, Pvent :
eta(V) = rendement instantané à la vitesse V = Pelec(V)/Pvent(V),
La puissance instantanée du vent
a été définie au début de cette page. Il reste à connaître la puissance
électrique débitée par l’éolienne en fonction de la vitesse V tout en
sachant que le détail des pertes successives à chaque étape de
transformation n’est pas explicité. En outre, si l’on peut connaître la
puissance électrique débitée en fonction de la vitesse de vent, on peut
évaluer la production électrique annuelle de l’éolienne sur base des
mesures du vent réalisées in situ :
Eelec = (Pelec(V)1 + Pelec(V)2 + … + Pelec(V)N)*dt.
La courbe caractéristique
de puissance d’une éolienne donne la puissance électrique en fonction
de la vitesse du vent. Généralement, ces courbes sont données par les
fabricants d’éoliennes. Dans le cas de grandes éoliennes, la courbe
caractéristique a été certifiée par un laboratoire et définie dans des
conditions d’essai standard. On a donc une certaine assurance quant aux
performances réelles de l’éolienne. La situation est plus critique pour
les petites éoliennes produites par de relativement petits
constructeurs. En effet, ils fournissent généralement la courbe
caractéristique de puissance de leur appareil, mais ils font rarement
certifier les performances. On n’a donc aucune ou peu d’assurance quant à
la fiabilité des performances annoncées. Dans tous les cas, la certification des performances
est un élément à bien garder à l’esprit lors de l’acquisition d’une
éolienne, surtout s’il s’agit de concepts novateurs ou
« potentiellement » révolutionnaires (pour ne pas dire fumants).
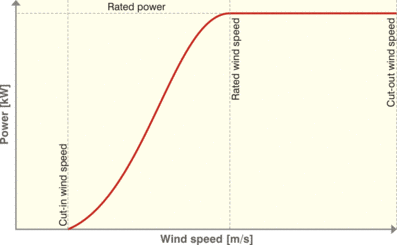
La courbe caractéristique de puissance comporte par trois grands paramètres (voir figure ci-dessous) :
- La vitesse minimale de démarrage (cut-in wind speed) : il s’agit de la vitesse du vent à partir de laquelle l’éolienne commence à débiter une puissance utile (c’est-à-dire de la puissance électrique).
- La vitesse maximale ou d’arrêt (cut-off wind speed) : il s’agit de la vitesse maximale acceptable par l’éolienne. Au-delà de celle-ci, la tenue mécanique de ces divers composants n’est plus assurée (ou simplement prévue). Si le vent présente une vitesse supérieure, l’éolienne est mise à l’arrêt, idéalement de manière automatique, pour préserver son intégrité.
- La puissance nominale (rated power) : cette valeur est souvent égale à la puissance électrique maximale qui peut être extraite de l’éolienne. Elle n’a jamais lieu à la vitesse maximale acceptable du vent. En effet, peu avant d’atteindre la vitesse de mise à l’arrêt, des dispositifs sont mis en place pour freiner la vitesse du rotor (soit de manière dynamique, soit de manière aérodynamique), ce qui peut diminuer significativement les performances de l’éolienne.

Forme typique d’une courbe de puissance
d’une éolienne : production électrique finale en kW en fonction de la
vitesse instantanée du vent en m/s.
Exemple : FairWind F64-40
À titre d’exemple, la société wallonne  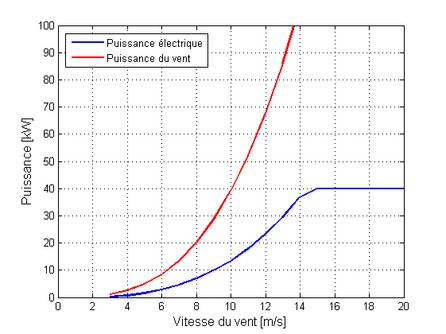 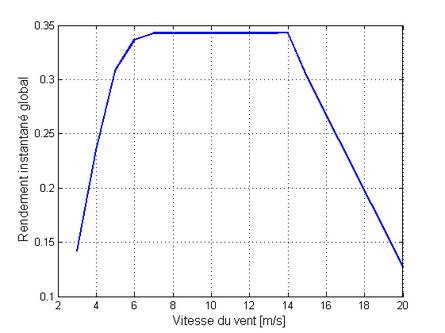
Performances de l’éolienne à axe vertical Fairwind F64-40 suivant les données fournies par le constructeur.
|
L’estimation de la production d’électricité
Sur base de mesuresSur base de la mesure du vent réalisée sur une période T et de la courbe caractéristique de puissance de l’éolienne, on peut évaluer la production électrique, Eelec, de l’éolienne durant cette période :
Eelec = (Pelec(V)1 + Pelec(V)2+ Pelec(V)3+ … + Pelec(V)N)*dt,
où on réalise une mesure de la vitesse toute les
« dt » secondes, on possède ainsi « N » valeurs dans notre échantillon
tel que T = N*dt. En bref, on suppose que la vitesse que l’on a mesurée à
un moment, Vi, reste constante pendant tout l’intervalle de mesure, dt. Durant un intervalle, l’éolienne produit Pelec(V)i*dt. On réalise finalement la somme sur tous les points de mesure pour obtenir l’énergie électrique finale.
Sur base de la distribution statistique
Une autre manière de procéder est de travailler sur base de la distribution statistique dont on connaît les paramètres (sur base de mesures ou de simulations) :
Eelec(V) = Pelec(V)*(p(V)*dV*T),
où, dans le membre de droite, le premier
facteur est la puissance électrique produite à la vitesse V et le second
facteur est le temps total durant lequel la vitesse est égale à V
(pendant la période de mesure, T). L’énergie finale, Eelec, est obtenue en sommant sur toutes les vitesses rencontrées.
Certains constructeurs utilisent cette méthode
pour communiquer une estimation de la production électrique annuelle de
leur éolienne. En fait, ils fixent les paramètres de la fonction de
distribution, p(V), et regardent ce que cela donne au niveau de la
production. Quand vous entendez des estimations de la production
électrique, il faut être conscient que le constructeur a fait des
hypothèses sur la manière dont les vitesses sont rencontrées dans le
temps. De manière générale, le vent sur votre site ne sera pas identique
à celui qu’il a considéré dans son estimation. Pour être rigoureux, il
faut veiller à ce que le constructeur communique ces paramètres. C’est
la seule manière de pouvoir comparer différents matériels entre eux sur
base d’estimation de la production électrique.
Estimation du rendement moyen global de l’éolienneOn peut aussi connaître le rendement moyen de l’éolienne sur la période d’observation, T. On peut estimer, d’un côté, l’énergie du vent qui était disponible (la source d’énergie), Event, et, d’un autre côté, l’énergie électrique produit par l’éolienne, Eelec (comme calculée ci-dessus). Le rapport de ces deux valeurs donne le rendement moyen :
Rendement moyen global = Eelec/Event,
Par global, on sous-entend que l’on s’intéresse à ce qui rentre et ce
qui sort globalement de l’éolienne. On trouve typiquement, un rendement
moyen de 20 % pour les petites éoliennes et de 35 % pour les grands
modèles.Nombre d’heures pleines de fonctionnementLa puissance débitée par une éolienne dépend de la vitesse du vent. Par conséquent, la majorité du temps, l’éolienne ne fonctionne pas à puissance nominale (PN), le vent n’étant généralement pas suffisant pour garantir cela. C’est un des arguments des détracteurs des éoliennes. En effet, comparé à des centrales électriques traditionnelles basées sur les énergies fossiles (typiquement une centrale TGV) ou le nucléaire qui peuvent fonctionner de manière continue proche de leur puissance nominale, une éolienne fonctionnera principalement à une puissance inférieure à PN. Du coup, il faudra une puissance installée supérieure avec des éoliennes qu’avec des centrales classiques pour atteindre une même production d’énergie annuelle. C’est un argument assez controversé bien que techniquement très clair. Le but n’est pas de faire le point sur ce sujet. On reprend juste ici l’argument.
Une manière de chiffrer la production d’une éolienne est de rapporter sa production électrique annuelle en nombre d’heures de fonctionnement à puissance nominale. En d’autres termes, on calcule le nombre d’heures que l’éolienne doit tourner à puissance nominale pour débiter la même production électrique annuelle (avec un vent dont la vitesse varie).
Nombres d’heures équivalentes à puissance nominale = tN = Eelec/PN.
Valeur typique pour les grandes éoliennes en Wallonie : tN = 25% de l’année.
Valeur typique pour le petit éolien en Wallonie tN = 11% de l’année.
Estimation rapide : Quick-scanDans certaines situations, notamment dans une étude de préfaisabilité, on souhaite pouvoir estimer grossièrement ce qu’un site va pouvoir donner comme production. On peut simplement se baser sur la vitesse moyenne du vent, Um, sur le site :
Estimation de la production = (rendement moyen global)*(1/2*rho*A*(Um)3),
où le rendement moyen est pris :- à 22 % pour le petit éolien (moins de 35 m de diamètre) ;
- 30 % pour l’éolien moyen (35 à 100 m de diamètre) ;
- et 35 % pour le grand éolien (> 100 m de diamètre).
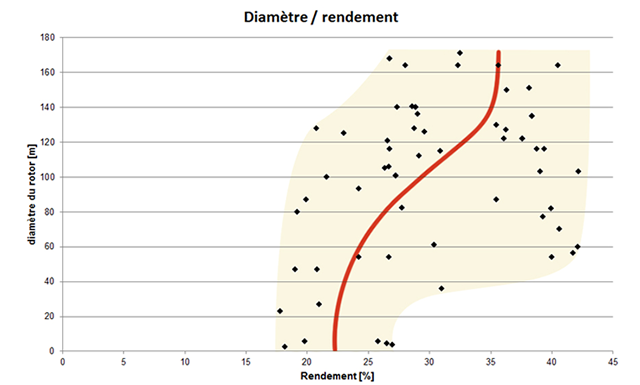
Dans la réalité, on remarquera une
tendance à un meilleur rendement pour les modèles d’éoliennes avec les
pales les plus longues (> 30 m) : diagramme réalisé sur base de 62 fiches techniques d’éoliennes récentes.
La limite de Betz
Le fabricant d’une éolienne doit faire certifier la courbe
caractéristique des performances de son modèle. Cela doit être réalisé
selon une méthode normalisée, idéalement par un laboratoire indépendant.
Dans la pratique, les modèles de plus faibles puissances ne bénéficient pas de cette certification. Le constructeur peut fournir une courbe de puissance, mais on n’a aucune garantie sur sa fiabilité, tout au plus, on peut se reposer sur la crédibilité du fabricant.
Comment détecter un produit farfelu ? Il n’y a malheureusement pas de méthode absolue (hormis tester le matériel). Néanmoins, certains chiffres communiqués par le constructeur peuvent être mis à l’épreuve. C’est le cas du rendement global instantané de l’éolienne tel que défini à la section précédente.
L’application des principes fondamentaux de la mécanique permet de déterminer la quantité maximale d’énergie du vent qui peut-être convertie en énergie mécanique (rotation du rotor). Ce rendement aérodynamique instantané, ou Coefficient de performance (Cp), ne peut dépasser 16/27 soit approximativement 59 %. Par conséquent, le rendement instantané qui tient aussi compte d’autres pertes (aérodynamiques, accouplement, conversion électrique, auxiliaires) doit être inférieur à cette valeur :
Dans la pratique, les modèles de plus faibles puissances ne bénéficient pas de cette certification. Le constructeur peut fournir une courbe de puissance, mais on n’a aucune garantie sur sa fiabilité, tout au plus, on peut se reposer sur la crédibilité du fabricant.
Comment détecter un produit farfelu ? Il n’y a malheureusement pas de méthode absolue (hormis tester le matériel). Néanmoins, certains chiffres communiqués par le constructeur peuvent être mis à l’épreuve. C’est le cas du rendement global instantané de l’éolienne tel que défini à la section précédente.
L’application des principes fondamentaux de la mécanique permet de déterminer la quantité maximale d’énergie du vent qui peut-être convertie en énergie mécanique (rotation du rotor). Ce rendement aérodynamique instantané, ou Coefficient de performance (Cp), ne peut dépasser 16/27 soit approximativement 59 %. Par conséquent, le rendement instantané qui tient aussi compte d’autres pertes (aérodynamiques, accouplement, conversion électrique, auxiliaires) doit être inférieur à cette valeur :
Rendement global instantané < rendement aérodynamique < 16/27
Cette limitation est mieux connue sous le nom de « limite de Betz »
ou « théorie de Betz ». Pour arriver à ces conclusions, il a fallu
introduire des hypothèses simplificatrices. Néanmoins, celles-ci sont
tout à fait raisonnables.Vitesse en bout d’aile et performance : tip speed ratio
On a vu que la limite de conversion de puissance du vent vers la
puissance mécanique du rotor est théoriquement limitée à 16/27, soit
59 %, par l’approche de Betz. Par rapport à ce cas idéal, il existe une
série d’imperfections qui empêchent d’atteindre cette limite. En
d’autres termes, on a une série de pertes qui réduisent l’efficacité
aérodynamique de l’éolienne :


Ces explications avaient juste vocation de montrer que le rendement
idéal n’était jamais atteint, ceci étant dû à différentes pertes. Un
facteur qui influence grandement ces pertes est le rapport entre la
vitesse en bout de pale (induite par la rotation) et la vitesse du vent,
le tip-speed ratio (TSR) en anglais, Lambda = tip-speed ratio (TSR) = u/V = n.2*pi*R/V,
- Mise en rotation du sillage : le vent avant de rencontrer l’éolienne ne possède pas de mouvement de rotation prononcé et cohérent. Du moins, c’est le cas s’il ne rencontre pas d’obstacles majeurs en amont de l’éolienne. Une fois que l’air est passé dans le rotor de l’éolienne, il en ressort avec une vitesse de rotation générale dans le sens opposé à celui du rotor. Cette vitesse de rotation qui n’existait pas au départ correspond à une certaine quantité d’énergie cinétique qui n’a pas pu être convertie pas l’éolienne. Il s’agit d’une première source de pertes.
- Trainée des profils de l’aile : lorsque l’on place une aile face au vent, il génère une force sur cette aile. C’est l’effet escompté. Cette force peut se décomposer en partie. Une force dite de portance qui est perpendiculaire à la direction du vent en aval de l’aile et une composante dite de trainée qui est parallèle à cette vitesse de vent. Dans le cas d’un avion, c’est la portance qui permet de vaincre la gravité et permet ainsi à l’avion de voler. La trainée freine l’avion, car cette force est opposée à la direction dans laquelle l’avion progresse. Pour permettre à l’avion de conserver cette vitesse, les moteurs de l’avion donnent la force nécessaire pour vaincre cette force de trainée. Dans le cas d’une éolienne, on retrouve la même idée. Néanmoins, il faut alors tenir compte à la fois de la vitesse du vent, mais aussi de la vitesse de rotation de l’éolienne. Le problème est un peu plus complexe. Tout cela pris en compte, on se rend compte que c’est la portance des pâles de l’éolienne qui exerce une force utile dans le sens de rotation de l’éolienne. La trainée des pâles, par contre, a tendance à freiner la progression de ces pâles. C’est une deuxième source de pertes parce qu’une partie de l’énergie du vent sert à freiner l’éolienne. Fort heureusement, une aile d’éolienne est conçue pour avoir la trainée la plus faible possible pour une portance donnée. En gros, il s’agit d’une question de spécialistes dans la mesure où il s’agit de travailler sur l’aérodynamique de l’aile.
- Nombre limité de pales : le nombre de pales d’une éolienne est limité pour des questions de poids et de prix. Le rendement idéal considéré plus haut faisait l’hypothèse d’un nombre très important de pales. Dans la réalité, ce nombre ne sera jamais atteint. Cette limitation est source d’une troisième forme de pertes. D’un point de vue physique, ces pertes sont générées par la trainée induite. La trainée induite est d’autant plus faible que la portance est faible et le rapport entre envergure et corde moyenne de l’aile est important. Ainsi, une aile qui a une grande envergure par rapport à la corde aura une trainée plus faible. On peut s’en convaincre en comparant les ailes d’un planeur à celle d’un avion traditionnel : les ailes du planeur sont beaucoup plus allongées pour limiter la trainée, ce qui est souhaitable étant donné qu’il n’a pas de moteur. C’est une des raisons qui expliquent pourquoi une éolienne a des ailes allongées.


Analogie entre l’allongement (aspect ratio) des ailes d’un planeur et des pales d’une éolienne : limitation de la trainée.
avec,
- u, la vitesse en bout de pale qui peut être évaluée comme étant le produit
- de la vitesse de rotation, n (en Hz),
- par le rayon de l’éolienne, R, multiplié par 2*pi.
- V est la vitesse du vent en amont.

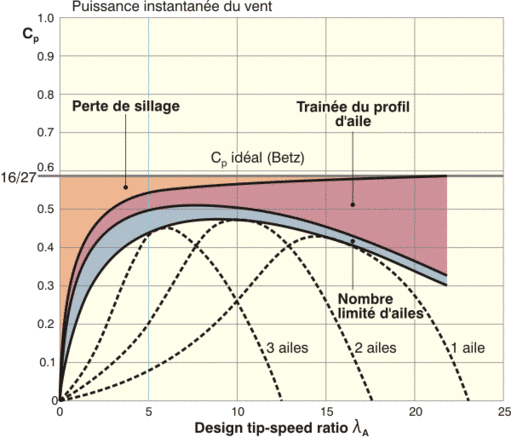
Évolution du rendement aérodynamique
instantané en fonction du rapport entre la vitesse en bout de pale et la
vitesse du vent (tip-speed ratio) : illustration des différentes
sources de pertes par rapport au rendement idéal de Betz.
On peut comprendre le graphe de la manière suivante :
- On dispose au départ de la puissance instantanée du vent par m², ce qui correspond dans le graphe au niveau de 100 %.
- La théorie de Betz nous apprend que l’on peut dans le meilleur des cas récupérer jusqu’à 16/27, soit approximativement 60 %.
- Si l’éolienne tourne plus lentement pour une vitesse de vent donnée, on aura un couple aérodynamique important pour atteindre une même puissance et donc une forte déviation du fluide par les pales. Cela engendre une mise en rotation plus importante du sillage et donc des pertes plus importantes. On le voit clairement dans le graphe sous la dénomination « pertes de sillage ». En conclusion, plus l’éolienne tourne vite, moins les pertes par mise en rotation sont importantes.
- Si on considère un profil d’une pale d’éolienne, la force aérodynamique se décompose en une force de portance, mais aussi de trainée qui s’oppose dans la direction de rotation de l’éolienne (du moins pour les éoliennes dont le principe de fonctionnement est basé sur la portance). L’effet négatif sur le rendement aérodynamique est d’autant plus important que l’éolienne tourne vite. On peut s’en rendre compte dans le graphe ci-dessus sous l’appellation « trainée du profil d’aile » où les pertes augmentent avec le tip-speed ratio. Sur base des deux premiers termes de pertes (pertes de sillage et de trainée de profil), on voit apparaître un premier optimum à une vitesse de relative de bout d’aile entre 6 et 8.
- On voit apparaître enfin le dernier terme de perte induit par le nombre limité de pales. En fait, si on prend la courbe relative à un nombre donné de pales en pointillé (on considère ici 1, 2 ou 3 ailes), on voit que la courbe générale correspond à l’enveloppe de tous les maxima des courbes à nombre de pâles fixé.

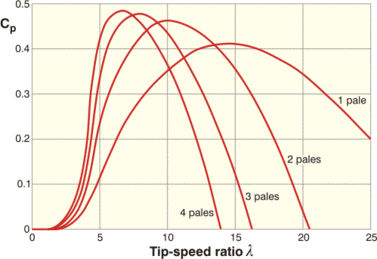
Évolution du rendement aérodynamique en fonction du nombre de pales pour un modèle donné.
Au regard de la courbe ci-dessus, qui reprend
l’évolution du rendement aérodynamique en fonction du nombre de pale
pour un modèle donné, on voit que plus le nombre de pales est important,
plus le rapport optimal de vitesse en bout de pale est faible.
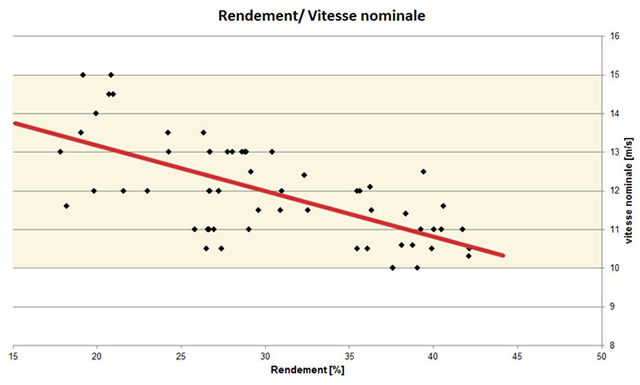
En outre, l’analyse des rendements de 62 modèles
récents d’éoliennes démontre qu’il y a une tendance claire vers un
meilleur rendement pour les éoliennes ayant une vitesse de vent nominale
plus basse (comprises entre 10 m/s et 12 m/s.

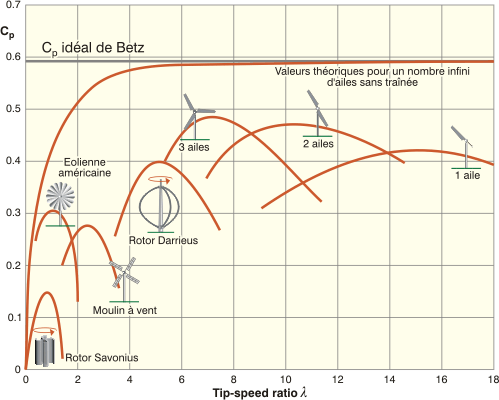
On peut conclure cette section en faisant une
description des différentes courbes caractéristiques de rendement
aérodynamique pour chaque grand modèle d’éolienne. De manière générale,
on voit que les éoliennes basées sur la portance, c’est-à-dire les
éoliennes à axe horizontal ou à axe vertical de type Darrieus, ont un
rendement aérodynamique supérieur aux éoliennes basées sur la trainée
(typiquement, le rotor Savonius). L’influence du nombre de pales sur le
rendement est aussi représentée. Si la vitesse de rotation diminue, il
faut un couple aérodynamique plus important pour une même puissance
mécanique. C’est pourquoi les éoliennes qui cherchent à produire du
travail mécanique, notamment pour des applications de pompage, ont un
nombre de pales important (illustré ci-dessous par l’éolienne
américaine). Actuellement, les éoliennes de type Darrieus ont un
rendement un peu supérieur à celui présenté dans le graphe ci-dessous.

Évolution typique du rendement aérodynamique en fonction du tip-speed ratio et du modèle d’éolienne.
php

Aucun commentaire:
Enregistrer un commentaire